画像の再構成理論④〜ノイズ拡大の原因〜

今回は画像の再構成理論の最終回として、ノイズ拡大の原因についてご紹介します。

画像の再構成で、前回、ガウシアンフィルタとなる行列[math]H[/math]を設定し、[math]d=Hs[/math]によってたたみこみを計算したと思います。今回は画像が繰り返しになっていると仮定して、ガウシアンフィルタとなる行列を自動的に設置するところからスタートします。

もう一度復習をしてみましょう。

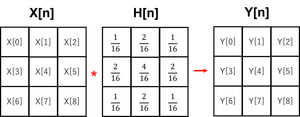
ガウシアンフィルタとのたたみこみにより Y_n が計算されます。たとえば Y_4 を計算するときには、

となります。

これはあくまで少ない次元の話でしたが、一般的な画像に関しても同じような計算をすることで、ガウシアンフィルタを設定することができます。

今回はちょうどよいサイズ（計算時間と見栄えとの兼ね合い）を考えて、 64 x 64の以下の画像について考えてみましょう。以下の実行にはpythonを用いてOpenCVを使います。

cv2.imread()で画像を呼び出し、for文によって画像を縦ベクトル s にします。画像のファイル名を"g01-1.tif"としています。

ためしに上のコードを実行すると画像が出力されると思います。これは縦ベクトルを二次元の画像の配列に戻しているのです。
これに、ガウシアンフィルタとなる演算をたたみこみます。以下のプログラムで 4096 x 4096 (64 x 64=4096)なる行列Hを生成しています。なお、画像の外側の影響は0にして考えています。