今回は、画像位置合わせに用いられるアフィン変換を紹介します。
アフィン変換とは、2つの画像における座標の線形変換を意味しており、拡大縮小、回転、平行移動を組み合わせた位置合わせに用いられます。
アフィン変換において、変換前の座標 (x_n, y_n) と変換後の座標 (X_n, Y_n) の関係は以下のように表されます。
アフィン変換とは、2つの画像における座標の線形変換を意味しており、拡大縮小、回転、平行移動を組み合わせた位置合わせに用いられます。
アフィン変換において、変換前の座標 (x_n, y_n) と変換後の座標 (X_n, Y_n) の関係は以下のように表されます。
この式を行列で表すと・・
このように、変換後行列は、アフィン変換行列と変換前行列の積としてと表わされます。
また、アフィン変換行列は、λ(拡大縮小率)、θ(回転角度)、(T_x),(T_y)(平行移動距離)を用いて上式のように表すことができます。
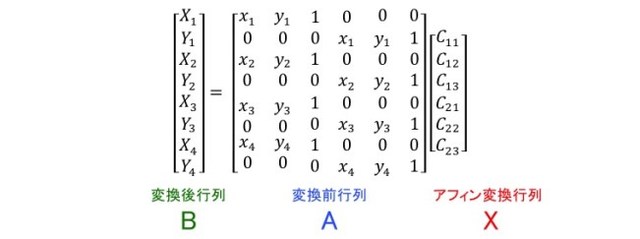
ここで、それぞれの行列の形や順番を入れ替えると、上と同じ意味の行列の関係式が下のように表せます(ここでは、特徴点4点を用いた変換を考えました)。形や順番は違えど、上式と同じことを表していることが確認できます。
また、アフィン変換行列は、λ(拡大縮小率)、θ(回転角度)、(T_x),(T_y)(平行移動距離)を用いて上式のように表すことができます。
ここで、それぞれの行列の形や順番を入れ替えると、上と同じ意味の行列の関係式が下のように表せます(ここでは、特徴点4点を用いた変換を考えました)。形や順番は違えど、上式と同じことを表していることが確認できます。
では、図1のような正方形の変換を考えてみましょう。
変換前(黒)がアフィン変換によって変換後(赤)になったとします。ただし、いずれも正方形の4つの頂点(特徴点)の座標しかわからず、どのような変換を施したのか分かりません。さて、どのような変換をしたのか、上の式を用いて解いていきましょう。
変換前(黒)がアフィン変換によって変換後(赤)になったとします。ただし、いずれも正方形の4つの頂点(特徴点)の座標しかわからず、どのような変換を施したのか分かりません。さて、どのような変換をしたのか、上の式を用いて解いていきましょう。
まず、上の行列に、変換前と後の正方形の座標の値を代入します。すると、下のようになります。
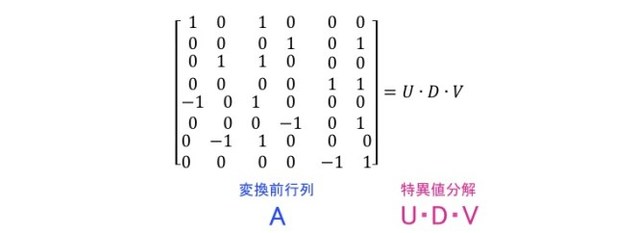
ここで、特異値分解と呼ばれる操作を施し、変換前行列 A を以下のように3つの行列の積に分解します(行列の計算や特異値分解についての詳細はこちら:http://www.iedu.i.kyoto-u.ac.jp/uploads/20141022.pdf)。
実際に、変換前行列 A を特異値分解した結果、それぞれの行列は下のようになりました(計算プログラムは後述)。










 木田智士
木田智士





