フーリエ変換は工学によって非常に重要な役割を果たしています。その応用分野は多岐にわたり、バリバリの物理の理論家さんから地震学者、生物系の研究者までです。これからの工学を支えていく上で確実に必要となるのがフーリエ変換なわけです。
今回のセクションの目標は「全ての信号は波の合成で表される」というフーリエ変換の本質を理解することです。
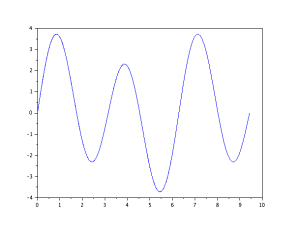
例えば以下のようなグラフがあったとします。
例えば以下のようなグラフがあったとします。
すでに波の形で表されていますね！図式化すると以下のようになります。
複雑なグラフも三角関数の足し算で表現出来る。
他にも例をあげておきます。
これは加法定理を用いることによって、以下のように分解することができるため、これも波として表されます。
これは加法定理を用いることによって、以下のように分解することができるため、これも波として表されます。
ここまでは普通に納得していただけると思います。波の足し算や波の掛け算で表されていると波の足し算に分解できるわけです。
それでは、 y=x^2 を波の合成で表すことはできるのでしょうか。
二次関数も波形に変換することが出来る？
このようなグラフが波の合成で表すことができるとは一見すると思えないと思います。しかし、可能なんです。
前回の記事で表したように離散フーリエ変換は以下のように表され、係数も積分で計算されたことが確認できたと思います。
前回の記事で表したように離散フーリエ変換は以下のように表され、係数も積分で計算されたことが確認できたと思います。
係数は以下のように計算されるのです。ここで積分が出てくるのは、上に表したように積分することによって求めたい部分のみが出てくるからです。
エルピクセル編集部
