こんにちは、今回は画像処理におけるフーリエ変換の3回目ということで、たたみこみについてお話ししたいと思います。
たたみこみはフーリエ変換を理解するためにも非常に重要な概念です。また確率過程の計算においてもたたみこみが用いられています。ここではたたみこみがどのように計算されるのか、そして、フィルターとはどういうものかについて話していきたいと思います。
復習にはなりますがImageJで実装してみましょう。ImageJを起動して画像を開いてください。(画像はクリックすると拡大します)
そして、command+shift+Dで複製をし、command+Aで全て選択、command+Xで消去してください。すると下のような画面になったと思います。
たたみこみはフーリエ変換を理解するためにも非常に重要な概念です。また確率過程の計算においてもたたみこみが用いられています。ここではたたみこみがどのように計算されるのか、そして、フィルターとはどういうものかについて話していきたいと思います。
復習にはなりますがImageJで実装してみましょう。ImageJを起動して画像を開いてください。(画像はクリックすると拡大します)
そして、command+shift+Dで複製をし、command+Aで全て選択、command+Xで消去してください。すると下のような画面になったと思います。
ここで、たたみこむ画像を作ります。Tool Boxからどれでも選び、任意の場所に図形を書いてください。
次にこれにcommand+Fで白くしてください。(灰色になることもあるようです)、それかcommand+ shift+I で画素値で反転してもOKです。
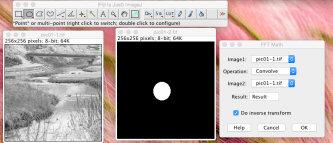
次にこれをたたみこみます。Process -> FFT -> FDMath からconvolveにするとたたみこむことができます。
次にこれをたたみこみます。Process -> FFT -> FDMath からconvolveにするとたたみこむことができます。
この場合は以下のようなピンボケ画像が得られたと思います。これは「画像の再構成理論①〜手ブレ、ピンボケ〜」でも説明したのと同じです。
ここで、この内部構造について説明していきましょう。以下は画像解析における畳み込み(http://www.clg.niigata-u.ac.jp/~medimg/practice_medical_imaging/imgproc_scion/4filter/index.htm
)を参考にしました。(少し式を訂正しました)
まず、一次元の信号において、たたみこみとは次のような演算です。
1.まずgの中心を注目する要素に合わせます。
2.注目する要素とgとをすべてかけます。
例えば注目する要素がcの場合、[cx,cy,cz]という組ができます。
3.すべての部分の足しあわせを行います。
例えばc'について計算する場合、c'は右から3番目であり、右から3番目の部分に影響を与えるのは、bを中心としたときのgの右側とcを中心としたときのgの中央とdを中心としたときのgの左側です。
ここで、この内部構造について説明していきましょう。以下は画像解析における畳み込み(http://www.clg.niigata-u.ac.jp/~medimg/practice_medical_imaging/imgproc_scion/4filter/index.htm
)を参考にしました。(少し式を訂正しました)
まず、一次元の信号において、たたみこみとは次のような演算です。
1.まずgの中心を注目する要素に合わせます。
2.注目する要素とgとをすべてかけます。
例えば注目する要素がcの場合、[cx,cy,cz]という組ができます。
3.すべての部分の足しあわせを行います。
例えばc'について計算する場合、c'は右から3番目であり、右から3番目の部分に影響を与えるのは、bを中心としたときのgの右側とcを中心としたときのgの中央とdを中心としたときのgの左側です。
それぞれについて計算すると以下のような結果が得られると思います。
ここで、なぜa'とg'は計算されていないのかと疑問に思う方もいらっしゃると思います。これは、画像の境界の外の設定の仕方によってその値が異なるからです。境界の外が繰り返しになっているか、それとも0かによってa',g'の値が違ってくることがわかります。
次に画像におけるたたみこみについて説明します。画像は信号が2次元になっただけで、1次元の信号と同じような計算によって畳み込みを実行することができます。
下に画像におけるたたみこみの計算例を一部示します。
次に画像におけるたたみこみについて説明します。画像は信号が2次元になっただけで、1次元の信号と同じような計算によって畳み込みを実行することができます。
下に画像におけるたたみこみの計算例を一部示します。
ある1ピクセルを計算するときの手順は一次元の信号と同じです。画像の場合2次元信号になっただけで、計算量は増えますが、同じような処理をすればよいことがわかります。
ここで、境界部分をどう計算するかについての条件が必要であることがわかります。ImageJのConvolutionはdefaultでは境界条件として繰り返しを採用しています。表示されている画像の外側にもタイル状に画像がいくつも並んでいるのをイメージしてください。具体的にどういうことかを説明したいと思います。
例えば、以下の二つの画像をたたみこむとしましょう。どんな画像が得られるのでしょうか?
ここで、境界部分をどう計算するかについての条件が必要であることがわかります。ImageJのConvolutionはdefaultでは境界条件として繰り返しを採用しています。表示されている画像の外側にもタイル状に画像がいくつも並んでいるのをイメージしてください。具体的にどういうことかを説明したいと思います。
例えば、以下の二つの画像をたたみこむとしましょう。どんな画像が得られるのでしょうか?





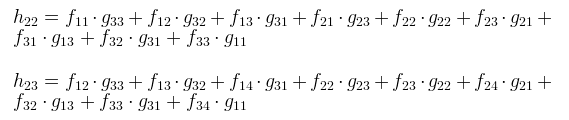






 エルピクセル編集部
エルピクセル編集部





