今度は範囲を 0 〜 2π ではなく、-π 〜 π で考えてみましょう。この場合も積分範囲が変化するだけです。
積分を計算する(部分積分を二回ほど行うと計算できる、興味のある人はやってみてください)と以下のように係数が決定されます。
積分を計算する(部分積分を二回ほど行うと計算できる、興味のある人はやってみてください)と以下のように係数が決定されます。
つまり、x^2は以下のように計算されるわけです。cos nxは波なので、波の合成で表されているわけです。これで、二次関数も三角関数の演算で表現されることが分かりました。式は以下のようになります。
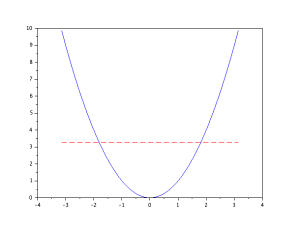
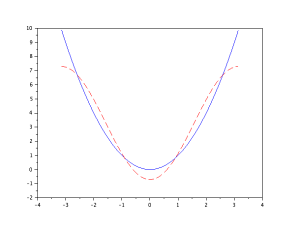
本当にこんな式で表されるのかな？と思う方がいらっしゃると思いますので、Σの部分を無限個の足し算ではなく、有限個にしてどのように近づいていくか、チェックしたいと思います。赤い点線がフーリエ級数です。
n=0のとき
n=1のとき
n=3のとき
n=5のとき
n=10のとき
n=100のとき
このようにnの値を増やしていくことで、フーリエ級数が二次関数の形に近づいていくことがわかると思います。x^2も波の合成で表すことができました。
まだ終わりではありません。
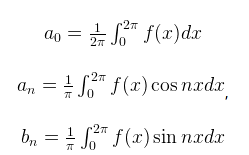
エルピクセル編集部
