この式は等号で結ばれているので、xに何を代入しても大丈夫です。
ここで両辺に x = π を代入してみましょう。左辺はπ^2になり、右辺のcosの方は (-1)^nになります。するとこの式は以下のように簡単になります。
この式を整理すると
このような方法でバーゼルの問題と呼ばれる18世紀の難問が解かれることになったわけです。こんな足し算が見事綺麗な値になるのはびっくりですよね！
今日は完全に数学のウンチクの話をしました。このようにフーリエ変換が純粋数学にも大きな貢献をしたということは注目すべきことのように思います。また時間があればこのような話も絡めて話していきたいと思います。
今日は完全に数学のウンチクの話をしました。このようにフーリエ変換が純粋数学にも大きな貢献をしたということは注目すべきことのように思います。また時間があればこのような話も絡めて話していきたいと思います。
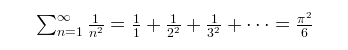
エルピクセル編集部
