今回は、前回紹介した相互情報量の概念を画像に応用し、実際のMRI画像を用いて相互情報量を計算することにより、画像の類似度を評価してみようと思います。
③ 2つの画像の相互情報量を求める
2つの画像A, Bにおける相互情報量とは、前回述べた相互情報量の考え方により、
「画像Aの画素値を知ることによって得られる画像Bの画素値についての情報量」ということになります。これはまさに、相互情報量が画像の類似度を表していることを示しています。例えば、2つの画像が全く同じならば、相互情報量は最大になり、2つの画像が全く無関係ならば、相互情報量はゼロになりますね。
簡単のため、2つの画像A, Bの画素値をいずれも 256階調(8bit)に変換しておきます。そして、全ての画素を網羅して、画素値の組み合わせ(a_i,b_j)の頻度を数え、それらをマッピングした2次元ヒストグラム h(a_i,b_j) を作ります。(ここでは、左上をヒストグラムの原点とし、横軸は画像Aの階調 a_i (i=1〜256)、縦軸は画像Bの階調 b_j (j=1〜256)とする。)
では、下のような脳MRI画像*(181×217 pixels)において、画像を回転させることによって2次元ヒストグラムや相互情報量がどのように変化するかを見てみましょう(計算プログラムは下に記載)。
「画像Aの画素値を知ることによって得られる画像Bの画素値についての情報量」ということになります。これはまさに、相互情報量が画像の類似度を表していることを示しています。例えば、2つの画像が全く同じならば、相互情報量は最大になり、2つの画像が全く無関係ならば、相互情報量はゼロになりますね。
簡単のため、2つの画像A, Bの画素値をいずれも 256階調(8bit)に変換しておきます。そして、全ての画素を網羅して、画素値の組み合わせ(a_i,b_j)の頻度を数え、それらをマッピングした2次元ヒストグラム h(a_i,b_j) を作ります。(ここでは、左上をヒストグラムの原点とし、横軸は画像Aの階調 a_i (i=1〜256)、縦軸は画像Bの階調 b_j (j=1〜256)とする。)
では、下のような脳MRI画像*(181×217 pixels)において、画像を回転させることによって2次元ヒストグラムや相互情報量がどのように変化するかを見てみましょう(計算プログラムは下に記載)。
図1. 元画像Aとそれを回転させた画像B(回転角度 = 0, 1, 2度)における2次元ヒストグラムと相互情報量
回転角度が0度の場合(つまり同じ画像同士)の2次元ヒストグラムは、図1右上に示すように傾きが-45°の直線になります。これは、どの画素においても、 a_i = b_jが成り立つことから理解できます。
回転角度を1度、2度と増やしていくと、直線から外れる点の数が増えてきているのがわかります。
では、画素値(a_i,b_j)の組み合わせが出現する確率 p(a_i,b_j) は、どのように表されるでしょうか?
回転角度を1度、2度と増やしていくと、直線から外れる点の数が増えてきているのがわかります。
では、画素値(a_i,b_j)の組み合わせが出現する確率 p(a_i,b_j) は、どのように表されるでしょうか?
上式のように、「ある画素値の組み合わせの頻度 / 全頻度」として、 h(a_i,b_j) を用いて表されます。
また、画素 a_i が出現する確率 p(a_i) , 画素 b_j が出現する確率 p(b_j)は、p(a_i,b_j) をそれぞれ縦方向、横方向に積分することによって、
また、画素 a_i が出現する確率 p(a_i) , 画素 b_j が出現する確率 p(b_j)は、p(a_i,b_j) をそれぞれ縦方向、横方向に積分することによって、
と表されます。
上の3つの確率を、前述の相互情報量 MI(A, B) の式
上の3つの確率を、前述の相互情報量 MI(A, B) の式
に代入することにより、相互情報量の値を求めることができます。(つまり、2次元ヒストグラムさえ得られれば、確率はそれを用いて全て求められ、相互情報量も求められます。)
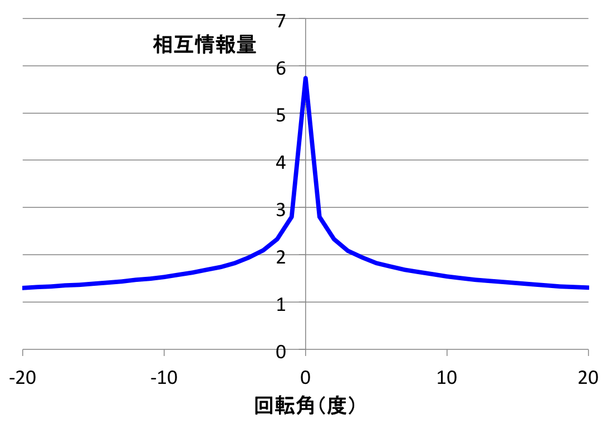
結果は、図1や図2に示すように、回転角度の絶対値が増すにつれて、相互情報量の値が減少するのが分かります。
結果は、図1や図2に示すように、回転角度の絶対値が増すにつれて、相互情報量の値が減少するのが分かります。
図2. 用いた脳MRI画像における回転角度(-20度~20度)と相互情報量との関係
相互情報量を求めるにあたり、pythonでプログラミングしましたので、参考にしてみてください。









 木田智士
木田智士



