今回は,前回(Part2.)に引き続き, 『パターン認識と機械学習』に沿って,機械学習の入門的なお話をまとめていきます.
前回は第1章の1.4節まで進めました.今回は1.5節の「決定理論」に関する内容をまとめます.
【機械学習で物事を“決定”する ~1.5節~】
生きていると,大なり小なり,何かしらの決断を迫られるときがあります. これは優柔不断な人にとっては特につらいものです. 雨が降りそうなのに,傘を持たずに家を出てしまった. 今から家に取りに戻ると会社に遅刻するかもしれない. そのまま会社に向かうとスーツが雨に濡れてしまうかもしれない. 不確定要素があると,どの選択がふさわしいか選びにくいものです. しかし,そのまま立ち尽くすわけにもいかず, 家に戻るか会社に向かうか,ひとまず“決定”する必要があります.
同じことは機械の中でも起こります. 多くの機械学習のアルゴリズムでは,「確率」を用いて予想を記述します. 「80%の確率で雨が降る」 「45%の確率でこの患者は肺がんである」 といった具合です. 数式を用いると,これは入力ベクトル$\bm{x}$が クラス $C_i$ に属する条件付確率 $p(C_i\mid \bm{x})$ として表されます. 手法によっては,同時分布$p(\bm{x},C_i)$を求める場合もあります. こういった確率分布を求めることを推論といいます.
しかし多くの応用例の場合,「確率」を求めて終わりではなく, 傘を取りに帰るか,肺がんの治療を行うか,など その後どのように行動するか決定する必要があります. 勿論,機械学習を行う限り,それは人間のカンに頼ったものではなく, 理論的に「尤もらしさ」が保証されたものでなければなりません. 今回は,この決定をどのように行うかについてお話します.
推論と決定:決定問題を解くための3種類のアプローチ
「決定問題」を解くアプローチは複数あり,3つに分類することができます. 簡単にその特徴を述べてみましょう.
- 丁寧に全て推論してから決定する. 複雑で面倒だが情報量が多い・応用性が高い
- ある程度推論して決定する.それなりに複雑だが,それなりに情報量がある
- 推論を飛ばして決定だけ行う.非常に単純だが,できることが制限される
もう少し具体的に説明します.
- A. 生成モデル
- クラスの条件付き密度 $p(\bm{x}\mid C_k)$, 事前クラス確率 $p(C_k)$ をすべて求めてしまう方法. するとクラス事後確率 $p(C_k\mid \bm{x})$ はベイズの定理から求まる. この方法は, 外部から $\bm{x}$ が与えられたときにそのクラス属性を決定できるだけでなく, モデルからサンプリングすることで人工的にデータ点 $\bm{x}$ を生成することもできる. このことから生成モデルと呼ばれる.
- B. 識別モデル
- 最初にクラス事後確率 $p(C_k\mid \bm{x})$ を求める. そのあと,後に述べる決定理論を用いて, $\bm{x}$ がどのクラスにふさわしいかを決定する. この手法は識別モデルまたは判別モデルと呼ばれる.
- C. 識別関数
- 各入力 $\bm{x}$ から, クラスラベルに写像する関数 $f(\bm{x})$ を直接見つける. たとえば2クラス分類問題なら,$f(\bm{x})$ は0,1の2値をとる. このアプローチでは,確率すら出てこない.
実際の応用では,この3種類のアプローチの全てが使われています.
言葉による説明だけでは違いがよく分からないという方もいるかもしれません. 以下,図を用いて違いを説明します.
識別モデル・識別関数の概念図
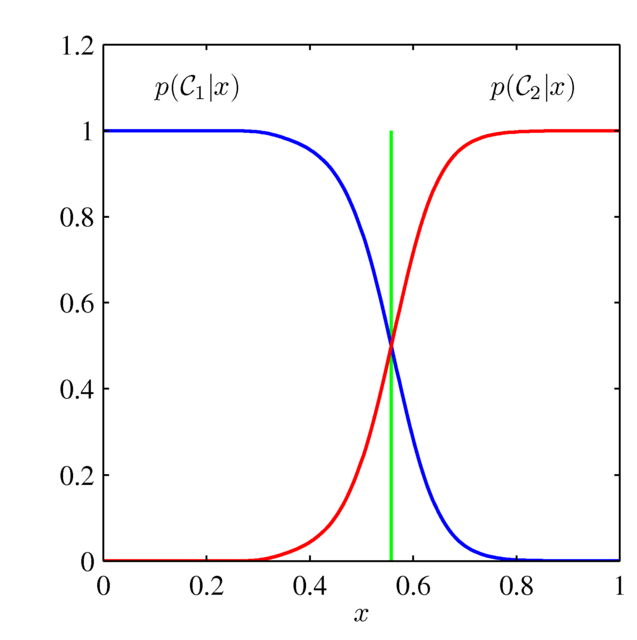
さらに,Cの識別関数を用いた方法では,「与えられた $\bm{x}$ でどのクラスが最も優勢か」という手がかりのみを与える.
したがって,上のモデルでCは実質「緑線が境界である」という情報のみ与え,赤や青の曲線の形状については何の手がかりも示さない.
※上の「生成モデル」とグラフの形こそ違うが,同一のモデルにかんする記述であることに注意.
ただし,$p(\bm{x})$ が未知である限り,こちらのグラフからはサンプリングによってデータ点を生成することはできない.
Aの生成モデルを求めてしまえばBで得られる手がかりはすぐ得られること, Bの識別モデルを求めてしまえばCの識別関数は(以下の決定理論によって) すぐ得られることに注意しましょう. その点で,モデルを記述する情報量という意味では, $\mathrm{A}> \mathrm{B}> \mathrm{C}$ ということになります. その分,求めるのにかかる手間もA,B,Cの順に大きいということですね.
あくまで決定が目的ならば, わざわざ生成モデルや事後確率なんて求める必要はない, いきなりCを実現してしまうのが最も簡便だ, と思うかもしれません. しかし,事後確率を計算すると,様々な事情を考慮して判断することができます. そのため,「事後確率をわざわざ計算したくなる」ことも多いのです. 様々な事情を考慮する方法は,以下の「決定理論」にて具体的に説明します.
決定理論:推論から決定を行うための様々な手法
先程述べたCの手法では,いきなり「識別関数」が求まります. これは「クラスを識別するための関数」としてすでに完成していますから, それ以上何かを行うことはありません.
一方で,A,Bの手法では,推論というプロセスによって 事後確率 $p(C_i\mid\bm{x})$ (データ点 $\bm{x}$ がクラス $C_i$ に属している確率) が求まります.つまり,「60%の確率で雨が降る」と分かっている状態です. ここから,傘を取りに戻るか決定する必要があります. A,B の手法を用いると,この決定段階に工夫を入れることができます.
最大事後確率による決定(誤識別率最小化)
推論から決定を行う場合,単純で直観的な方針は, 「最も事後確率 $p(C_i\mid\bm{x})$ の高いものに従って決定を行う」というものです. たとえば 「この画像は,30%の確率で犬,45%の確率で猫,25%の確率で鳥の画像である」 と推論できているとすれば, その画像は「猫」の画像だと結論付けるのが最も妥当だということになります.
とてもアタリマエのような,直観的な話だと思うかもしれません. 実は「誤識別率の最小化」という観点から, 理論的にも妥当であることが知られています(詳しい説明は割愛します).






 最上 伸一
最上 伸一






すなわち $p(C_i)$ および $p(\bm{x}\mid C_i)$ の形すら推定する.
ベイズの定理を用いれば,このグラフから $p(C_i\mid \bm{x})$ を求めることができる(それが下図となる).
また上のグラフを用いれば,上の確率分布にのっとって「サンプリング」することによって,学習結果に従う $\bm{x}$ の人工的なデータ点を生成することができる.