【機械学習勉強会】パターン認識と機械学習(PRML)第1章のまとめ Part.1

こんにちは！新しく記事を書かせていただくことになった，最上伸一です． 今まさに私が「学習」している最中の機械学習理論について，これから くわしくお話したいと思います．

機械学習やAI，最近何かと話題になっているから少し勉強してみたけど， 何が何やらさっぱり分からない…という人向けに， 機械学習のアレやコレを，なるべく分かりやすく解説していきます！

機械学習理論をまとめる上で軸にした本が，名著と名高い『パターン認識と機械学習』． 機械学習に興味があって色々調べていれば，ご存知の方も多いかと思います． 英語で ``Pattern Recognition and Machine Learning" だから，PRMLという通称で呼ばれています．

そもそも，「機械学習」とは何でしょうか． また，機械学習を実行するということは，具体的にどのような手続きを指すのでしょうか．

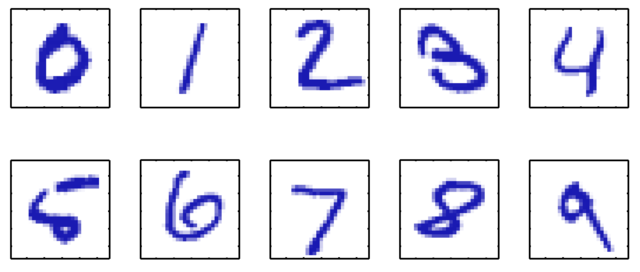
私たち人間は，とても自然に学習を行っています．たとえば，ここに 手書き数字の「4」があったとしましょう． それが自分の書いた字ではなく，自分のクセとは多少違っていたとしても （たとえば，4の上をぴったり付けて書くか離して書くかなど）， 私たちは「4」という数字だと認識することができます．

同じことを機械が行うのは大変です． 4という数字の書き方のルールは，厳密に定まっていないからです． 無理にルールを教えようとしても，そのルールに当てはまらない「4」や， そのルールに当てはまってしまう「4でないもの」が沢山出てきてしまい， ルールと例外を果てしなく追加しなければなりません （これをルール数が発散すると表現しています）．

人力で見つけ出された経験的な規則 （こういう発見的規則のことをヒューリスティックな規則といいます） では，機械にうまく伝わりません． そこで，機械が扱う規則性は，機械に発見してもらうことにします． これが機械学習です．

機械学習の目標は，ある入力ベクトルに対して，適切な出力を返せるようになること． 上の例では，「手書き文字」という入力ベクトルから，「数字」という出力を返すのが目標です． 何か入力が与えられたときに出力が定まるもののことを， 数学の世界では関数と言うのでした．まさに，

機械学習は多くの場合，「学ぶ」段階を経て， 「学んだことを活用する」段階に移ります． 学ぶ段階を訓練段階や学習段階といい， 学習に用いるデータを訓練データといいます． 学んだことを活用するときに用いるデータをテストデータといいます． 人間も，授業で学んだ（訓練した）ことを確かめるとき，テストを行いますよね． テストデータに用いられるものは，訓練データと全く同じものばかりではありません． 訓練と異なる新たな事例を分類する能力のことを，汎化といいます．

機械学習には大きく分けて3種類あります． 教師あり学習と教師なし学習， そしてその中間ぐらいの立場をとる強化学習です．

ここでいう「教師」とは，「正解」とか「お手本」ぐらいの意味でとらえると分かりやすいと思います． 先程の文字認識の例では，「これは4と認識してほしい」という正解があるため， 教師あり学習を行うのが妥当です．

まずは代表的な機械学習の例として，回帰問題を考えましょう． 回帰とは，与えられた入力ベクトルから1つ以上の連続的な数値を予測することです． 機械学習的な考え方でいうと， 「予め与えられた入力ベクトル（訓練データ）から，目標値が従う規則性を見つけ出し， 目標値が分からない入力ベクトル（テストデータ）にその規則性に当てはめて，未知の目標値を予測する」 わけですから，教師あり学習を行うことになります．ここでいう教師は，目標値のことですね．

たとえば最高気温と湿度のデータから，あるアイスクリームの売り上げを予測したいとします． このとき入力ベクトルは「最高気温と湿度」，目標値はアイスクリームの売り上げです． そこから，たとえば気温と湿度が高ければアイスクリームが良く売れる，といった規則性を見つけ出し， およそどういう数式に従うのか予測するのが回帰です．

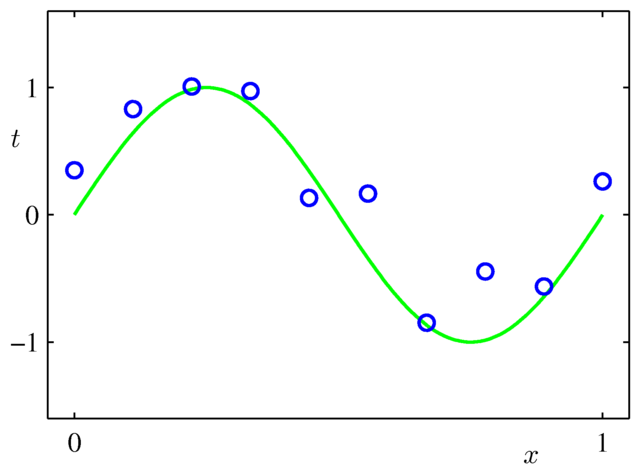
もう少し具体的に話をするために，人工的に作られた，次のデータを考えてみましょう．

この青い点は，$y=\sin(2\pi x)$ にランダムなノイズを入れて作られています． もっとたくさんデータ点を取れば，青い点だけから $y=\sin(2\pi x)$ がうっすら見えてきますが， ここではたった10個の点から，$y=\sin(2\pi x)$ のような規則性をできるかぎり正確に予測することを目標にしましょう．

回帰問題で最も単純なのは線形回帰と呼ばれる，一次関数で近似する方法ですが， 今回予測したいデータは（青い点だけを見ても）ぐにゃぐにゃと折れ曲がっているように見えますから， ここは多項式曲線フィッティングを考えることにします．つまり，規則性を \begin{align} y(x,\bm{w})=w_0+w_1x+w_2x^2+\cdots+w_Mx^M \end{align} という形の式，$M$ 次関数で予想してみます． $\bm w$ というのはベクトル $(w_0,w_1,\ldots,w_M)$ のことです． 慣習的に，太字は基本的にベクトルを表します．

具体的にどのように予測するかですが，次の二乗誤差と呼ばれる値： \begin{align} E(\bm{w})=\dfrac{1}{2}\sum_{n=1}^N\bigl(y(x_n,\bm{w})-t_n\bigr)^2 \end{align} を最小化するように，うまく $\bm{w}$ の値を決めます． $y(x_n,\bm{w})-t_n$ というのは，真の値($t_n$)と予測値($y(x_n,\bm{w})$)とのズレ． 直観的には，「なるべくデータ点とのズレの総和が小さくなるような $\bm w$ を見つける」ということです． この $\bm w$ をどうやって見つけるかについては…今回は割愛します．

さて，ここで問題です． $M$ 次関数でフィッティングするとき，私たちはまず $M$ の値を決める必要があります． 次の3つのうち，$y=\sin(2\pi x)$ への当てはまりが最も良くなるのはどれでしょうか．

• 1次関数でフィッティング（つまり線形回帰）
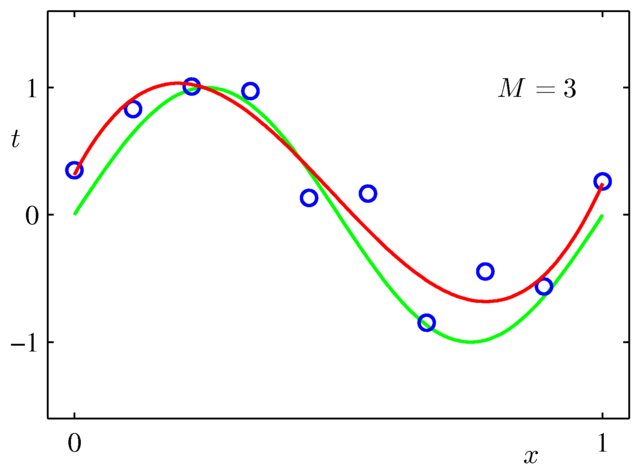
• 3次関数でフィッティング
• 9次関数でフィッティング

皆さん，予想は出来ましたか？

百聞は一見に如かず，ということで， 実際に多項式をあてはめた結果を見てみましょう．