コンピュータビジョンの領域において、動いている画像の特徴点を見つけ、同じものや人間であることを特定することはとても重要な問題である。
少しでも違う向きを向いていたら、本人と認識出来なかったり、違うものとプログラムが認識してしまうと、顔認識や物体認識としては用を成さなくなるからだ。
そこで、3次元以上の情報を抽出し、その物体の特徴点を認識することが出来れば、より精度の高い画像認識を行うことが出来る。
過去には、図形の3x3の行列を用いて平面上の特徴量を調べるアフィン変換や、2点から見た映像から3次元的な位置を特定するエピポーラ幾何などが用いられてきたが、3次元のテンソル上で画像を認識することで、より精度の高い認識が出来る。
具体的には、3次元以上のすべての特徴量の組合せを多重線形関数の最大化として定式化することでグラフマッチングさせようとしている。この関数は特徴量の組の間の類似度として定義される。
多重線形関数というのは、一見すると難しいが、与えられた数値情報などが様々な相関関係を持っていることを示している。どの値をXに、どの値をYとして関数をつくるか、その組み合わせが1つでなく沢山ある。このような線形的な量または線形的な幾何概念を一般化したものをテンソルと呼ぶ。
少しでも違う向きを向いていたら、本人と認識出来なかったり、違うものとプログラムが認識してしまうと、顔認識や物体認識としては用を成さなくなるからだ。
そこで、3次元以上の情報を抽出し、その物体の特徴点を認識することが出来れば、より精度の高い画像認識を行うことが出来る。
過去には、図形の3x3の行列を用いて平面上の特徴量を調べるアフィン変換や、2点から見た映像から3次元的な位置を特定するエピポーラ幾何などが用いられてきたが、3次元のテンソル上で画像を認識することで、より精度の高い認識が出来る。
具体的には、3次元以上のすべての特徴量の組合せを多重線形関数の最大化として定式化することでグラフマッチングさせようとしている。この関数は特徴量の組の間の類似度として定義される。
多重線形関数というのは、一見すると難しいが、与えられた数値情報などが様々な相関関係を持っていることを示している。どの値をXに、どの値をYとして関数をつくるか、その組み合わせが1つでなく沢山ある。このような線形的な量または線形的な幾何概念を一般化したものをテンソルと呼ぶ。
(出典:Wikipedia)
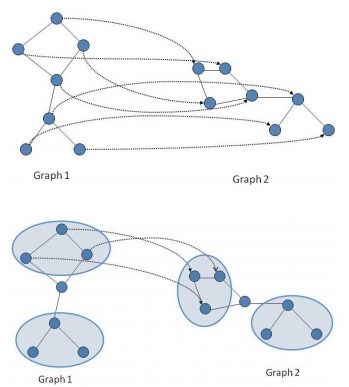
ここで、論文で紹介されている図形を見てみよう。
これらの2つの図形は、それぞれの点同士の位置や距離もそれぞれ全く異なる。1~2次元での類似度の解釈は難しいように思われる。
しかし、それぞれの点の位置の変化をテンソルとして捉えれば、どの点が対応するかが分かる。
このように特徴点の類似性を示したテンソルを用いて関数を定義して、グラフマッチングを行ったのが今回の論文である。
特徴点のスペクトル法の一般化を使って期待値の最大化を行った。多次元べき乗法によって解かれ、次に最近傍の割り当て行列に投影された。
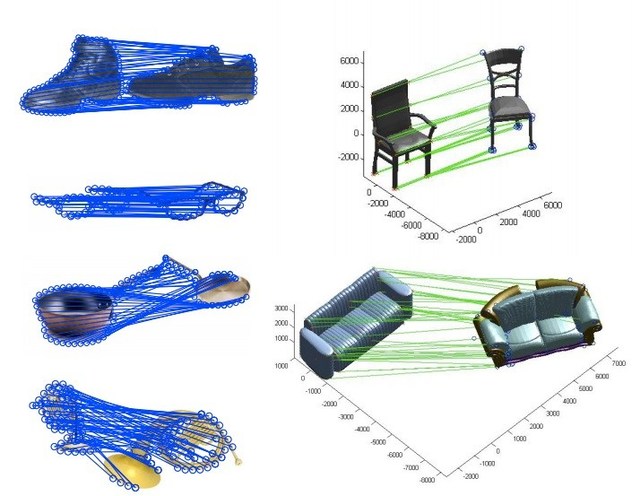
実際にこの手法を用いて、画像のグラフマッチングを行った実例も紹介されている。
しかし、それぞれの点の位置の変化をテンソルとして捉えれば、どの点が対応するかが分かる。
このように特徴点の類似性を示したテンソルを用いて関数を定義して、グラフマッチングを行ったのが今回の論文である。
特徴点のスペクトル法の一般化を使って期待値の最大化を行った。多次元べき乗法によって解かれ、次に最近傍の割り当て行列に投影された。
実際にこの手法を用いて、画像のグラフマッチングを行った実例も紹介されている。
同様の研究を日本でも行われているようなので、参考資料にて紹介する。
<参考資料>
A Tensor-Based Algorithm for High-Order Graph Matching
高次のグラフマッチングのためのテンソルに基づくアルゴリズム (Ricoh Abstract Club)
エピポーラ幾何(大人になってからの再学習 はてなブログ)
アフィン変換(画像処理ソリューション FC2)
物体認識のための 3 次元特徴量の基礎と動向(中京大学大学院 情報科学研究科 橋本 学 ビジョン技術の実利用ワークショップ)
テンソルベース3次元立体認識(立命館大学 陳研究室)
<参考資料>
A Tensor-Based Algorithm for High-Order Graph Matching
高次のグラフマッチングのためのテンソルに基づくアルゴリズム (Ricoh Abstract Club)
エピポーラ幾何(大人になってからの再学習 はてなブログ)
アフィン変換(画像処理ソリューション FC2)
物体認識のための 3 次元特徴量の基礎と動向(中京大学大学院 情報科学研究科 橋本 学 ビジョン技術の実利用ワークショップ)
テンソルベース3次元立体認識(立命館大学 陳研究室)
8 件






 エルピクセル編集部
エルピクセル編集部





