def teta(z,tau,c): # c = 0 or 1 c = np.double(c)/2 n_max = 100.0 + c pi = np.pi t = 0.0 + 0.0j; for n in np.linspace(-n_max,n_max,2*n_max+1): t = t + np.exp(pi*1j* n*n*tau + 2*pi*n*1j*z) return t def teta01(z,tau): t = teta(z+1.0/2,tau,0) return t def teta11(z,tau): t = teta(z+1.0/2,tau,1) return t def teta10(z,tau): t = teta(z,tau,1) return t def teta00(z,tau): t = teta(z,tau,0) return t def cn(u,k): # k -> tau # Reference: Wikipedia # https://ja.wikipedia.org/wiki/%E3%83%A4%E3%82%B3%E3%83%93%E3%81%AE%E6%A5%95%E5%86%86%E9%96%A2%E6%95%B0 k_dash = np.sqrt(1.0 - k*k) l = 1.0/2 * (1.0 - np.sqrt(k_dash))/(1.0 + np.sqrt(k_dash)) q = l + 2*np.power(l,5) + 15*np.power(l,9) + 150*np.power(l,13) + 1707*np.power(l,17) tau = np.log(q) / (np.pi * 1j) # calculate t10 = teta10(0.0+0.0j , tau) t00 = teta00(0.0+0.0j , tau) t01 = teta01(0.0+0.0j, tau) # check print(np.sqrt(1.0 - np.power(t01/t00,4) )) = k z = u/(np.pi* t00 * t00) return t01 * teta10(z,tau) / (t10*teta01(z,tau)) Ke = sp.special.ellipk(1.0/2) def schw_chrf(z): # reference: https://arxiv.org/pdf/1509.06344.pdf return (1.0 - 1.0j)/np.sqrt(2) * cn( Ke*(1.0+1.0j)/2 * z - Ke, 1.0/np.sqrt(2))
\begin{align} \vartheta(z,\tau) = \sum_{n=-\infty}^{\infty} \exp\left(\pi i n^2 \tau + 2\pi i n z \right) \end{align}
$q = \exp(\pi i \tau)$として
\begin{align} \vartheta_0(z,\tau) &:= \vartheta_{01}(z, \tau) = \sum_{n=-\infty}^{\infty} e^{\pi i \tau n^{2} + 2 \pi i n \left(z + \frac{1}{2}\right)} =1 + 2 \sum_{n=1}^{\infty} (-1)^{n} q^{n^{2}} \cos 2 n \pi z \end{align} \begin{align} \vartheta_{1}(z, \tau) &:= - \vartheta_{11}(z, \tau) = - \sum_{n=-\infty}^{\infty} e^{\pi i \tau \left(n + \frac{1}{2}\right)^{2} + 2 \pi i \left(n + \frac{1}{2}\right) \left(z + \frac{1}{2}\right)} =2\sum_{n=0}^{\infty}{(-1)^{n} q^{{\left(n + \frac{1}{2}\right)}^2} \sin(2 n + 1) \pi z} \end{align} \begin{align} \vartheta_{2}(z, \tau) &:= \vartheta_{10}(z, \tau) = \sum_{n=-\infty}^{\infty} e^{\pi i \tau \left(n + \frac{1}{2}\right)^2 + 2 \pi i \left(n + \frac{1}{2}\right)z} = 2 \sum_{n=0}^{\infty} q^{{\left(n+\frac{1}{2}\right)}^2} \cos (2 n + 1) \pi z \end{align} \begin{align} \vartheta_3(z, \tau) &:= \vartheta_{00}(z, \tau) = \sum_{n=-\infty}^{\infty} e^{i \pi \tau n^{2} + 2 \pi i n z} = 1 + 2 \sum_{n=1}^{\infty} q^{n^{2}} \cos 2 n \pi z. \end{align}
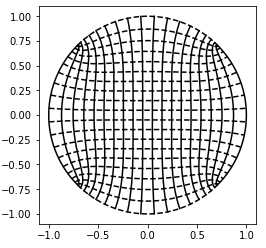
for x_i in x_m: z_h = x_i*np.ones(m) + x*1j z_v = x+1j*x_i*np.ones(m) w_h = schw_chrf(z_h) w_v = schw_chrf(z_v) plt.plot(np.real(w_h),np.imag(w_h),color='black') plt.plot(np.real(w_v),np.imag(w_v),color='black', linestyle='dashed') plt.gca().set_aspect('equal', adjustable='box') sc = 1.1 plt.xlim(-s*sc,s*sc) plt.ylim(-s*sc,s*sc) plt.show()
4. 画像への適用
今回用いるのは,このような将棋の画像です.
# load image img = cv2.imread('picture_c/base200.png') #img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY) # show image with matplotlib pix = img.shape[0] x = np.linspace(-1,1,pix+1) # define square plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)) plt.gray()
# text mapping # schwartz christoffel mapping import sys for i in range(pix): sys.stdout.write(str(i)) sys.stdout.write(" ") for j in range(pix): tx_z = np.array([x[i],x[i+1],x[i+1],x[i]]) ty_z = np.array([x[j],x[j],x[j+1],x[j+1]]) zt = tx_z + 1j*ty_z w_h = schw_chrf(zt) tx = np.real(w_h) ty = np.imag(w_h) clr_b = np.double(img[ pix - j - 1 , i,0])/256 clr_g = np.double(img[pix - j - 1 , i,1])/256 clr_r = np.double(img[pix - j - 1 , i,2])/256 plt.fill(tx,ty,color=(clr_r,clr_g,clr_b)) plt.gca().set_aspect('equal', adjustable='box') sc = 1.1 plt.xlim(-s*sc,s*sc) plt.ylim(-s*sc,s*sc) plt.show() plt.savefig("output/base.png")







 エルピクセル編集部
エルピクセル編集部





