はじめに
先日,量子アニーリングの勉強会に参加して来ました.そのアウトプットとして,今回,数独ソルバーを作成しました.数独を解く方針は以下の通りです.
- 処理1.与えられた数字を元に各マスに入りうる数字を考える.その個数が1つであれば,それをマスに入れる.
- 処理2.各マスに入りうる数字がすべて複数個となるまで1を繰り返す.
- 処理3.各マスに入りうる数字を列挙する.
- 処理4.数字を仮置きして1と2を繰り返す.途中で矛盾が生じたら仮置きをやり直す.
- 処理5.完成
処理1,2,3では量子アニーリングを使わず,処理4で量子アニーリングを使用しました.
実装
check_line 関数:列または行を確認してマスに入りうる数字を返す
check_block 関数:3×3のブロックを確認してマスに入りうる数字を返す
solve_quiz 関数:処理1,2を行う
check_block 関数:3×3のブロックを確認してマスに入りうる数字を返す
solve_quiz 関数:処理1,2を行う
import numpy as np import pandas as pd from sympy import * import re import wildqat def check_line(quiz_, id_row): digit = [1,2,3,4,5,6,7,8,9] digit_fill = quiz_[id_row][quiz_[id_row]>0] digit_blank = np.setdiff1d(digit, digit_fill) return digit_blank #------------------------------------------------------------------------------------------------ def check_block(quiz_, id_row, id_col): id_row = id_row // 3 id_col = id_col // 3 quiz_block = quiz_.reshape((3,3,3,3))[id_row, :, id_col] digit = [1,2,3,4,5,6,7,8,9] digit_fill = quiz_block[quiz_block>0] digit_blank = np.setdiff1d(digit, digit_fill) return digit_blank #------------------------------------------------------------------------------------------------ def solve_quiz(quiz_): id_blank = [] while True: #---- if 'len(id_blank)' is the same as the previous loop, 'while loop' ends if len(id_blank) == len(np.array(np.where(quiz_==0)).T): break #---- obtain 'candidate' that can be filled in the blank #---- then, if the number of 'candidate' is one, fill in the blank id_blank = np.array(np.where(quiz_==0)).T for id_blank_row, id_blank_col in id_blank: candidate_row = check_line(quiz_, id_blank_row) candidate_col = check_line(quiz_.T, id_blank_col) candidate_block = check_block(quiz_, id_blank_row, id_blank_col) candidate_concat = np.concatenate((candidate_row, candidate_col, candidate_block)) candidate_unique = np.unique(candidate_concat, return_counts=True) candidate = candidate_unique[0][candidate_unique[1]==3] if len(candidate) == 1: quiz_[id_blank_row, id_blank_col] = int(candidate) return quiz_
その1.py
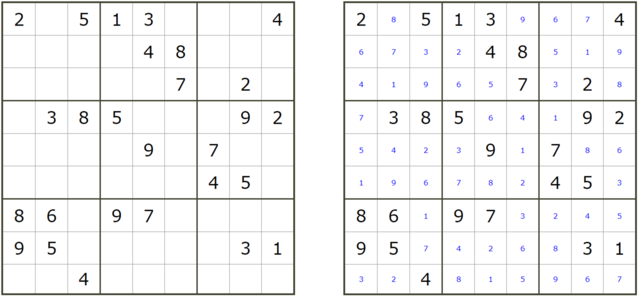
問題と解答を設定し,処理1および2を行います.
quiz = np.array([
[2,0,5,1,3,0,0,0,4],
[0,0,0,0,4,8,0,0,0],
[0,0,0,0,0,7,0,2,0],
[0,3,8,5,0,0,0,9,2],
[0,0,0,0,9,0,7,0,0],
[0,0,0,0,0,0,4,5,0],
[8,6,0,9,7,0,0,0,0],
[9,5,0,0,0,0,0,3,1],
[0,0,4,0,0,0,0,0,0]
], dtype=object)
sol = np.array([
[2,8,5,1,3,9,6,7,4],
[6,7,3,2,4,8,5,1,9],
[4,1,9,6,5,7,3,2,8],
[7,3,8,5,6,4,1,9,2],
[5,4,2,3,9,1,7,8,6],
[1,9,6,7,8,2,4,5,3],
[8,6,1,9,7,3,2,4,5],
[9,5,7,4,2,6,8,3,1],
[3,2,4,8,1,5,9,6,7]
], dtype=object)
quiz = solve_quiz(quiz)その2.py
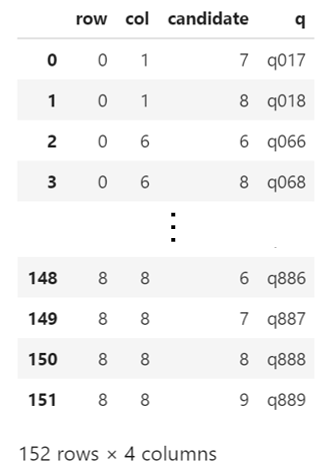
「処理3.各マスに入りうる数字を列挙する.」を行います.
id_blank = np.array(np.where(quiz==0)).T candidate_li = [] row_li = [] col_li = [] q_li = [] for id_blank_row, id_blank_col in id_blank: candidates_row = check_line(quiz, id_blank_row) candidates_col = check_line(quiz.T, id_blank_col) candidates_block = check_block(quiz, id_blank_row, id_blank_col) candidates_concat = np.concatenate((candidates_row, candidates_col, candidates_block)) candidates_unique = np.unique(candidates_concat, return_counts=True) candidates = candidates_unique[0][candidates_unique[1]==3] for candidate in candidates: row_li.append(id_blank_row) col_li.append(id_blank_col) candidate_li.append(candidate) q_li.append('q{}{}{}'.format(str(id_blank_row), str(id_blank_col), str(candidate))) df = pd.DataFrame({ 'row': row_li, 'col': col_li, 'candidate': candidate_li, 'q': q_li })
その3.py
次の制約を使って立式します.
制約1.1つのマスに入りうる数字の中から1つだけ選んだ場合,0となる
制約2.1行で数字が重複しない場合,0となる
制約3.1列で数字が重複しない場合,0となる
制約4.3×3のブロック内で数字が重複しない場合,0となる
制約1.1つのマスに入りうる数字の中から1つだけ選んだ場合,0となる
制約2.1行で数字が重複しない場合,0となる
制約3.1列で数字が重複しない場合,0となる
制約4.3×3のブロック内で数字が重複しない場合,0となる
E = 0 #---- define (Σqi -1)**2 for each cells for row, col in df.loc[:, ['row', 'col']].drop_duplicates().values: f=0 for q in df.loc[(df['row']==row) & (df['col']==col), 'q'].tolist(): f += Symbol(q) f -= 1 f = f**2 E += expand(f) #---- define (Σqi - 1)**2 for each rows for row in range(9): df_row = df.loc[df['row']==row, :] for candidate in df_row['candidate'].unique(): f = 0 for q in df_row.loc[df_row['candidate']==candidate, 'q'].tolist(): f += Symbol(q) f -= 1 f = f**2 E += expand(f) #---- define (Σqi - 1)**2 for each cols for col in range(9): df_col = df.loc[df['col']==col, :] for candidate in df_col['candidate'].unique(): f = 0 for q in df_col.loc[df_col['candidate']==candidate, 'q'].tolist(): f += Symbol(q) f -= 1 f = f**2 E += expand(f) #---- define (Σqi - 1)**2 for each blocks for row in [[0,1,2], [3,4,5], [6,7,8]]: for col in [[0,1,2], [3,4,5], [6,7,8]]: df_block = df.loc[(df['row']>=min(row)) & (df['row']<=max(row)) & (df['col']>=min(col)) & (df['col']<=max(col))] for candidate in df_block['candidate'].unique(): f = 0 for q in df_block.loc[df_block['candidate']==candidate, 'q'].tolist(): f += Symbol(q) f -= 1 f = f**2 E += expand(f)
その4.py







 井上 大輝
井上 大輝





