先日,インターンのみんなで「パターン認識と機械学習(上)」の第1章の輪読会を行いました.
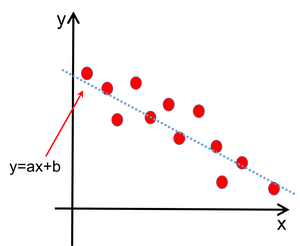
輪読会の中で主に議論となったのは,多項式フィッティング. 多項式フィッティングとは,たくさんあるデータ点を多項式で表現する,というものです. 例えば,下の図を見てください. 散布図に当てはまりの良い直線 $y=ax+b$ を引いています.
上の例では直線,つまり一次関数を考えていますが, 「多項式」と言うわけですから,一般には何次の関数でも同じことができます. $N$ 次の関数を仮定すれば, \begin{align} y=w_0+w_1x+\cdots +w_Nx^N \end{align} という形で書くことができます.この形に統一するなら,先ほどの直線 $y=ax+b$ は \begin{align} y=w_0+w_1x \end{align} に相当します.ここまではOKですよね! 直線の例は,結局1次多項式の例を考えていたにすぎない,というわけです.
では,データ点にちょうどうまくフィットするようなパラメータ $a,b$ は どうやったら見つけられるのでしょうか?
ここで係数を求める方法が, 最小二乗法と呼ばれる方法です. 最小二乗法とは
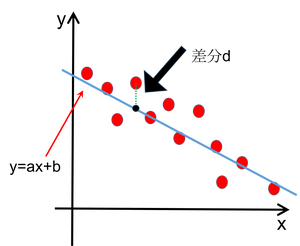
というものです.下図を見てイメージをつかんでください. 点線部分が「差分」に相当します. この差分 $d$ の二乗を全てのデータ点について計算して足しあわせ, それが最も小さくなるように係数を設定するとよい.これが最小二乗法です.
一般に,$M$ 点からなるデータがそれぞれ $(x_i,y_i)$ と表されており, これを $N$ 次の多項式でフィッティングすることを考える場合,差分 $d$ は \begin{align} d&=y_i-(w_0+w_1{x_i}+\cdots+w_N{x_i}^N)\notag\\ &=y_i-\sum_{k=0}^Nw_k{x_i}^k \end{align} と表されますから,全ての差分の2乗の総和は \begin{align} S(w_0,\ldots,w_N)=\dfrac{1}{2}\sum_{i=1}^M\left(y_i-\sum_{k=0}^Nw_k{x_i}^k\right)^2 \end{align} となります.$\dfrac{1}{2}$ というのは,後々の都合を考えて便宜上つけたものです.
これを最小にすれば,求めたい多項式の係数 $w_k$ が得られる,ということがわかりますね! しかし,ここからが問題です. どうやってこの $S(w_0,\ldots,w_N)$ を最小にするものを求めるのでしょうか.
当てずっぽう,では到底無理ですよね. なぜなら,決定するべきパラメータがたくさんあるからです.
もしもパラメータが1つしかなかったら,最小値を求めるのは比較的簡単です. 例えば, \begin{align} f(w)=w^2+4w+1 \end{align} の値を最小にするものを求めたいとき,どのようにするでしょうか.
こういうときに強力な力を発揮するツールが微分です. 微分とは,大雑把に言えば傾きのこと. 二次関数ならその関数の傾きが0になるところが最小値となるだろう,と予測できるわけです.
上の関数を微分してみると \begin{align} f'(w)=2w+4 \end{align} となり,この値が0になるのは $w=-2$ のときだから, $f(w)$ は $w=-2$ の時に最小になる,と瞬時に求まるわけです.
実は,この微分するという方針,これはパラメータが沢山あっても使えます. では今回の最小二乗法の場合,何を微分すればよいのでしょうか. 決定したい変数は,多項式フィッティングの係数 $w_0,\ldots,w_N$ です. 先程,一変数の場合は「パラメータ$w$」で微分することで 目的のパラメータの値が分かるのでした. その類推で,今回も $w_0$ から $w_N$ までで微分すればよいのか,と想像ができます. そうなんです.しかし,$N+1$ 個も微分するのは確実に大変ですね.
ここで導入するのが,「ベクトルで微分を行う」という方法です. が,今回は長くなったのでひとまず休憩し, 次の章からベクトルでの微分について考えていきます.







 エルピクセル編集部
エルピクセル編集部





