本記事では,最近注目を集めているベイズ統計について,Rでの実装を行います.具体的な内容としては,平均値の差の推定を行います.今回は,Rstan をというライブラリを用いるのですが,環境構築に関してはRstanの公式Githubが日本語訳されているので,こちらを参考して頂けると良いかと思います.https://github.com/stan-dev/rstan/wiki/RStan-Getting-Started-(Japanese)
そして今回は,以下の例題を考えます.
そして今回は,以下の例題を考えます.
[例題] とある学校の X組と Y組におけるテストの平均点を比較する. X組に属する20人の点数は [49 , 66 , 69 , 55 , 54 , 72 , 51 , 76 , 40 , 62 , 66 , 51 , 59 , 68 , 66 , 57 , 53 , 66 , 58 , 57] 平均59.8点で, Y組に属する20人の点数は [41 , 55 , 21 , 49 , 53 , 50 , 52 , 67 , 54 , 69 , 57 , 48 , 31 , 52 , 56 , 50 , 46 , 38 , 62 , 59] 平均50.5点であった.このとき X組と Y組の平均点および点数差の事後分布を求めよ.
まず前提条件として,標本X および Y は,平均がそれぞれ μx と μy (母平均),かつ分散 σ² (母分散) が等しい正規分布に従う母集団から無作為抽出されたと考えます.それぞれを式で表すと,
となります.また,母数の集まりは,
であります.次に尤度は,「母平均および母分散が与えられたとき (を知っていたとすると),今回の標本が得られる確率」であり,次の式で表されます.
となります.最後に,事前分布は,
で表されます.以上より,事後分布を,
の式で表すことができます.この式を利用して, MCMC法を用いることで,正規化定数の解析的計算は必要なくなり,母数 θ の事後分布に従う乱数の生成が可能となります.MCMC法によって得られた事後分布を以下に示します.この事後分布から様々な統計量が得られます.まず,X組およびY組の平均値の事後分布 (a) をみると,期待値 (X組:59.72,Y組:50.47) と分散 (X組:2.33,Y組:2.32) となりました.今回の場合,90,000回サンプリング操作を繰り返しています.その中で,x < y を満たす回数を数え,サンプリングの回数 (今回の場合は 90,000) で割れば,「X組の真の平均値 < Y組の真の平均値」となる確率を求めることができ,0.997 という値が算出されました.続いて,真の平均値の差 が 95 % の確率で含まれる区間は,平均値の差の事後確率分布 (b) で 95 % のデータが含まれる範囲を計算すると算出でき,これを 95 % ベイズ確信区間と呼び,本例題では,2.77 > μx - μy > 15.69 が得られました.
# データを受け取る
data {
int<lower=0> N_x;
int<lower=0> N_y;
real<lower=0> x[N_x];
real<lower=0> y[N_y];
}
# 平均および分散を定義
parameters {
real mu_x;
real mu_y;
real<lower=0> sigma;
}
#事前分布を定義
model {
mu_x ~ normal(0, 100);
mu_y ~ normal(0, 100);
sigma ~ cauchy(0, 5);
x ~ normal(mu_x, sigma);
y ~ normal(mu_y, sigma);
}
# 統計量を定義.今回は平均値の差
generated quantities {
real diff;
diff = mu_x - mu_y;
}
bayesian_inference.stan
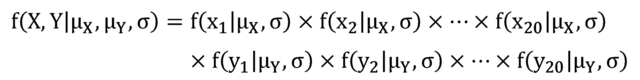

 井上 大輝
井上 大輝





