CTの詳しい原理について話していこうと思います.
CTというと,既に完成された技術のように思いますが,「投影回数を少なくしたい!」かつ,「様々な方向から投影できない!」という場合にも対応できるように,より精密に断面を再構成する技術が求められています.
CTというと,既に完成された技術のように思いますが,「投影回数を少なくしたい!」かつ,「様々な方向から投影できない!」という場合にも対応できるように,より精密に断面を再構成する技術が求められています.
目次
・CT とは
・CTの原理
・Radon変換のmatlab のプログラム
・CTの原理
・Radon変換のmatlab のプログラム
1. CT とは
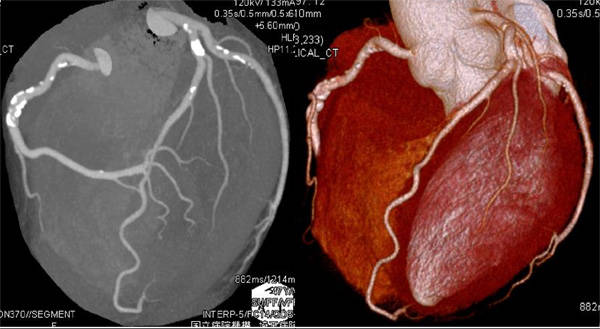
CTとは,Computed Tomography の頭文字をとったもので,コンピュータ断層撮像法と訳されます. CT検査とは,X線をつかって身体の断面を撮影する検査です. X線を照射し,断面を通過したデータを集め,画像処理を行うことで,断面を再構成します.
CTの応用分野は非常に広く,医療系であれば「カテーテルX線血管造影法」,「CTアンジオグラフィ」,「三次元欠陥撮影」(参考文献[1]),工業系であれば「非破壊検査」,「CAE」,「デジタルエンジニアリング」などがあります.
2. CTの原理
さて,それではCTの原理について説明していきましょう.
CTは,X線を目的の物体に照射し,それの減衰を見ることによって,物体の形状を再構成する手法です.
投影する領域全体での減衰率$f(x,y)$を復元します.
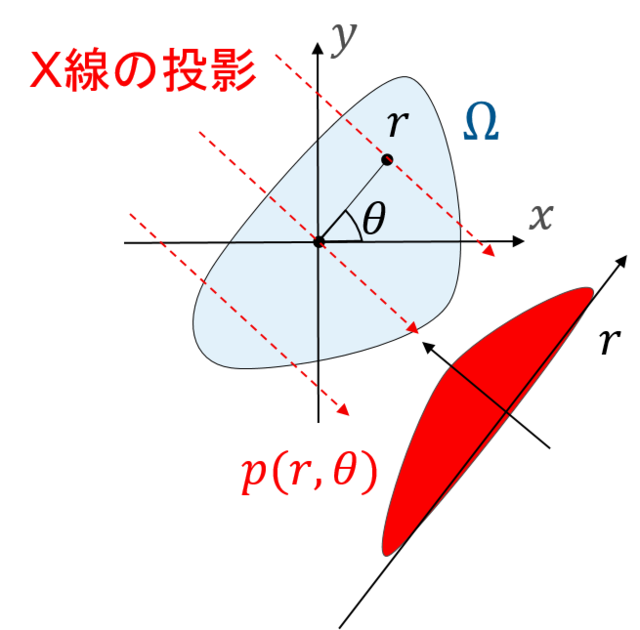
図の角度$\theta$から$\Omega$へ投影し,それにより得られる積分量は以下のように記述されます.
\[
p(r,\theta) = \int_\Omega f(x,y) \delta(r-x \cos \theta - y\sin\theta)d xdy
\]
様々な角度$\theta$からの投影により,$f(x,y)$を完全に求めることが目的です.
この$p(r,\theta)$が観測量です.
関数$p(r,\theta)$を$f(x,y)$のラドン変換と呼びます.
この$\delta(r)$というのはディラックのデルタ関数と呼ばれる関数であり,可積分な関数$f(x)$
に対して
\[
\int_{-\infty}^{\infty} \delta(x) f(x) dx = f(0)
\]
となるようなものです.
$\delta$の中身が$0$になるところだけ出現すると考えてもらってよいです.
上での積分は,デルタ関数の定義から,物体を$\theta$方向から投影した総和が得られることがわかります.
3. Radon 変換のプログラム
以下,少しだけmatlab のコードを載せたいと思います.
ラドン変換などの原理の理解の一助となれば幸いです.
ラドン変換などの原理の理解の一助となれば幸いです.
まず,サンプルデータをロードします.
P = phantom(256); imshow(P)
load_phantom.mat
次にラドン変換をしてみます.






 エルピクセル編集部
エルピクセル編集部





