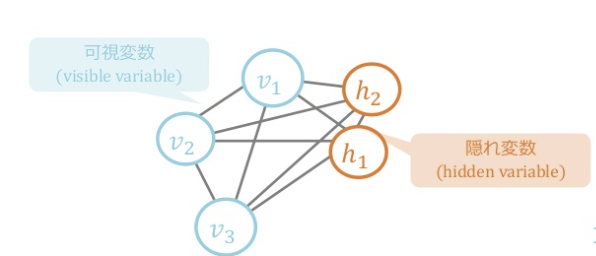
これは、「高い自由度を持ち、隠れ変数を十分にとると任意の分布を近似できる 」ことがしられています。
隠れBoltzmann Machine
隠れ変数$h_{i}$が追加されています。
エネルギー関数は上と同じです。$h$を追加したものに関して同じようなエネルギー関数を定義します。
\begin{align}
\phi(z) =- \sum_{i} b_{i}z_{i} - \sum_{i,j}w_{ij} z_{i}z_{j}
\end{align}
$z$は$v$と$h$をつなげたものです。
\begin{align}
\phi(z) =- \sum_{i} b_{i}z_{i} - \sum_{i,j}w_{ij} z_{i}z_{j}
\end{align}
$z$は$v$と$h$をつなげたものです。
一般にこれは学習が非常に困難になります。そこで考案されたのが、RBMです。
つまり、上のモデルにある「制約」を加えるわけです。
長くなったので、続きはまた次回にします。
つまり、上のモデルにある「制約」を加えるわけです。
長くなったので、続きはまた次回にします。
via pixabay.com
エルピクセル編集部
