画像処理におけるスパースモデリング
画像のスパースモデリングとは スパース:「疎ら」 なモデリングを行う,ということです.このようなスパースモデリングは,画像処理にとどまらずノイズ除去や,領域のセグメンテーションなどに用いられています.
ここでは,画像処理において,スパースモデリングとはどういうことを意味するのか,pythonを用いてコーディングを行います.
1. L1 正則化に基づく画像の再構成
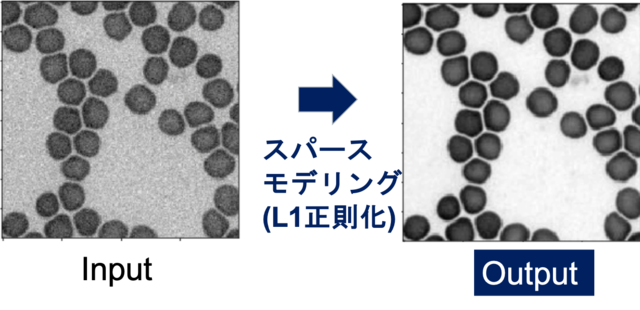
L1画像の再構成では,具体的に以下のような評価関数の最小化を考えます. Input の画像から Outputの画像に変換します.
\begin{align} F = \frac{1}{2} |I_{input} - I_{output}|^2 + \lambda |I_{output}|_{1} \end{align}
この評価関数の第一項目は入力画像と出力画像の2乗誤差です.これは,Input画像とOutput画像が明らかに違うようなものは求めてない,ということです.
大事なのは第二項目です.この項は$I_{input}$のL1ノルムに対応します.L1ノルムの最小化はスパースな解,つまり要素として0を多く含む解が得られるようになります.今回の場合,$I_{output}$のL1ノルムの最小化を行っているので,$I_{output}$の画素の多くが0になるような Output を得ることができます.
なお,0ではなく別の値$A$の値をスパースにしたいときなどは,上の評価関数を
\begin{align} F = \frac{1}{2} |I_{input} - I_{output}|^2 + \lambda |I_{output} - A|_{1} \end{align} とすることで解決できます.上のように,バックグラウンドの値は白なので,GrayScale の画像では$A=255$とする必要がありますね.
2. Total Variationに基づく画像の再構成
上のL1ノルムの最小化は,バックグラウンドのノイズを除去するのに使われます.これは,背景部分がほとんどある値$A$になっているだろう,という仮定によるものでした.
それでは次に,以下のような評価関数を考えてみましょう.
\begin{align} F’ = \frac{1}{2} |I_{input} - I_{output}|^2 + \lambda |\nabla I_{output}| \end{align}
ただし, $ |\nabla I_{output}| = | \nabla_x I_{output}| + | \nabla_y I_{output}| $ の和であり,$ \nabla_x I_{output} $は$ I_{output} $の隣接するピクセルの$x$方向の差分です.この正則化をTotal Variation (以下TV)正則化と呼びます.
今度の正則化はOutput 画像の画素の隣接ピクセルの差分に関する正則化です.差分のL1をとっているため,差分がスパースつまり画素値の変化が画像内で少なくなるような効果を生み出します.
具体的には以下のような画像のノイズを削減しようとするときに,この正則化を用いることで解決できます.
Python による実装
それでは,この最適化をプログラムしてみましょう. ただし,L1ノルム正則化の最適化問題は,簡単には実装できません. 最適化問題を解く方法として,様々な方法が提案されていますが,この記事では Split Bregman 法 により最適化を行います.
1. L1正則化の場合
評価関数を再度記述すると以下のようになります.
\begin{align} F = \frac{1}{2} |I_{input} - I_{output}|^2 + \lambda |I_{output}|_{1} \end{align}
これを最小化する解は,実は陽に書くことができます.それを具体的に示していきましょう.
評価関数の変数を単純化します. \begin{align} F = \frac{1}{2} |x - b|^2 + \lambda |x|_{1} \end{align}
上の評価関数を要素ごとの和で書き表すと
\begin{align} F = \frac{1}{2}\sum_{i} (x_i - b_i)^2 + \lambda \sum_{i} |x_{i}| \end{align}
が得られます.よって,各変数$x_i$に関して最小化を行えばよいことが分かります.
次に,$x_i=a_i e_i$,$a_i>0,\ e_i=1,\ or, \ -1$とします.つまり,$x_i$を符号のIndicator $e_i$と大きさを表す$a_i$に分割します.これを用いると,上の式は
\begin{align} F = \frac{1}{2}\sum_{i} (a_i e_i - b_i)^2 + \lambda \sum_{i} a_i \end{align} となります.
ここで,$a_i>0$に注意します.$(a_i e_i - b_i)^2$をできるだけ小さくしたいのですが,$b_i$と$e_i$とがもし異符号であれば,$(a_ie_i - b_i)^2 > b_i^2$となります.よって,最小化したいのであれば,$e_i = {\rm sgn}(b_i)$となることが分かります.
このように$e_i$が求まれば,あとは$a_i$に関する最小化を行うことで解決します.具体的には
\begin{align} F = \frac{1}{2}\sum_{i} (a_i {\rm sgn}(b_i) - b_i)^2 + \lambda \sum_{i} a_i \end{align} \begin{align} = \frac{1}{2}\sum_{i} (a_i - |b_i|)^2 + \lambda \sum_{i} a_i \end{align} \begin{align} = \frac{1}{2}\sum_{i} (a_i - |b_i| + \lambda )^2 + 2\lambda|b_i| - \lambda^2 \end{align}
これから,$a_i>0$に注意して,
\begin{align} a_i = {\rm max} (|b_i|-\lambda,0) \end{align} という解が得られます.
つまり.L1ノルムの制約付き最小化問題では,このように設定することで,解が得られることが分かります.正則化パラメータを調整することで,L1ノルムの最適化問題を解くことができます.

 エルピクセル編集部
エルピクセル編集部





